Best Mathematician

In the vast realm of mathematics, where abstract concepts and intricate theories thrive, identifying the "best" mathematician is an intriguing yet challenging endeavor. The discipline of mathematics has evolved over centuries, with countless brilliant minds contributing to its growth and development. This article aims to delve into the lives and contributions of some of the most influential mathematicians, shedding light on their remarkable achievements and the profound impact they have had on the field.
The Titans of Mathematics
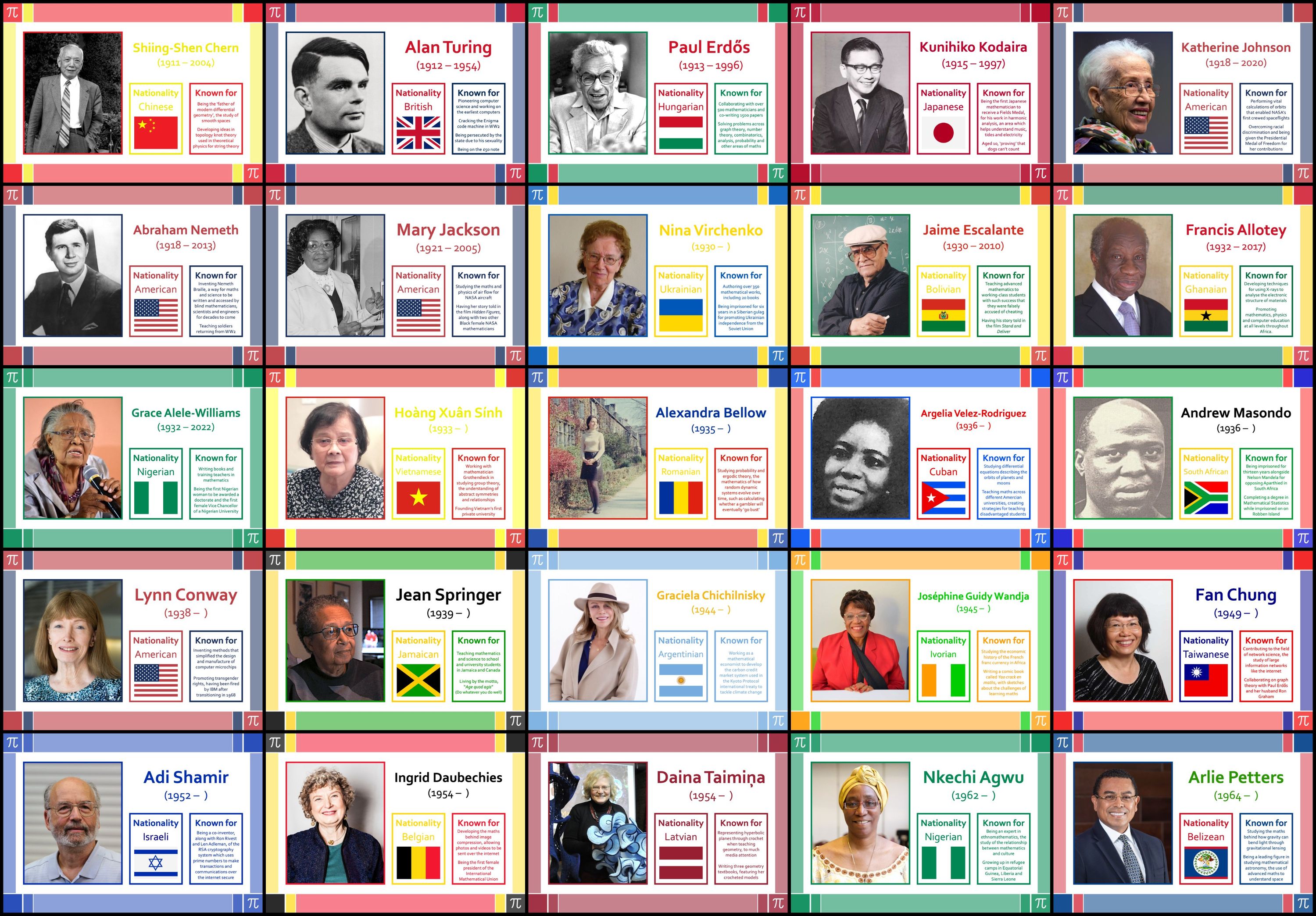
The world of mathematics boasts an array of brilliant minds, each with their unique genius and contributions. Here, we showcase a few of these mathematical titans and explore their significant impact on the discipline.
Isaac Newton: The Pioneer of Modern Mathematics
Sir Isaac Newton, an English physicist and mathematician, is often regarded as one of the most influential scientists of all time. His contributions to mathematics are nothing short of revolutionary. Newton’s seminal work, Philosophiæ Naturalis Principia Mathematica, laid the foundation for classical mechanics, gravitation, and calculus.
Newton's invention of calculus, a branch of mathematics that deals with continuous change, is arguably his most significant mathematical contribution. Calculus provided mathematicians and scientists with powerful tools to solve complex problems, revolutionizing fields such as physics, engineering, and economics. His laws of motion and universal gravitation also had a profound impact on our understanding of the physical world.
In addition to his mathematical prowess, Newton's work on optics and his development of the reflecting telescope further solidified his legacy as a scientific luminary. His ability to seamlessly blend mathematical and scientific principles remains a testament to his genius.
Carl Friedrich Gauss: The Prince of Mathematicians
Carl Friedrich Gauss, a German mathematician and physicist, is often referred to as the “Prince of Mathematicians” due to his vast and profound contributions to the field. Gauss’ work spanned a wide range of mathematical disciplines, including number theory, statistics, and astronomy.
One of Gauss' most notable achievements was his proof of the fundamental theorem of algebra, which states that every non-constant single-variable polynomial with complex coefficients has at least one complex root. This proof, considered by many as one of the most elegant in mathematics, showcased Gauss' exceptional mathematical insight.
Gauss' contributions to number theory are also significant. He developed the theory of quadratic reciprocity, a result that provides insight into the solvability of certain polynomial equations. His work on the least squares method, a statistical technique for estimating relationships between variables, is another landmark contribution.
| Mathematical Contribution | Description |
|---|---|
| Fundamental Theorem of Algebra | Proof that every polynomial equation has a solution. |
| Quadratic Reciprocity | A result in number theory, aiding in the understanding of polynomial equations. |
| Least Squares Method | A statistical technique for estimating relationships between variables. |

Gauss' mathematical genius extended beyond pure mathematics. He made significant contributions to geodesy, the study of the Earth's shape and gravitational field, and his work on the calculation of orbits influenced astronomy for decades.
Leonhard Euler: The Master of Mathematical Elegance
Leonhard Euler, a Swiss mathematician and physicist, is renowned for his prolific contributions to mathematics and his ability to express complex ideas with remarkable simplicity. Euler’s work covered a vast array of mathematical topics, making him one of the most influential mathematicians in history.
Euler's greatest contributions lie in the fields of geometry, trigonometry, and number theory. His work on analytic geometry, especially his introduction of Cartesian coordinates, revolutionized the way mathematicians approached geometric problems. He also made significant advancements in complex analysis, developing new techniques and methods that are still in use today.
Euler's formula, eiπ + 1 = 0, is considered one of the most beautiful and profound formulas in mathematics. It links five fundamental mathematical constants: e (the base of the natural logarithm), π (the ratio of a circle's circumference to its diameter), i (the imaginary unit), 1, and 0. This formula, simple yet elegant, encapsulates the beauty of mathematical harmony.
Other Mathematical Luminaries
The world of mathematics is rich with brilliant minds, and the mathematicians mentioned above are just a few of the many who have left an indelible mark on the discipline. Here’s a brief glimpse into the lives and works of a few more mathematical giants:
- Archimedes of Syracuse: An ancient Greek mathematician, physicist, and inventor, Archimedes is known for his contributions to the fields of mathematics, physics, and engineering. His work on hydrostatics, the principle of buoyancy, and his invention of various war machines during the Roman siege of Syracuse are particularly notable.
- René Descartes: A French philosopher, mathematician, and scientist, Descartes is often regarded as the father of modern Western philosophy. In mathematics, he is known for his work on the Cartesian coordinate system, which allowed for the graphical representation of algebraic equations.
- Alan Turing: An English mathematician, computer scientist, and cryptanalyst, Turing is often considered the father of computer science and artificial intelligence. His work on the Turing machine, a theoretical device that can simulate the logic of any computer algorithm, laid the foundation for modern computing.
The Impact and Legacy of Mathematical Giants

The influence of these mathematical luminaries extends far beyond their respective lifetimes. Their contributions have shaped the course of mathematics and have had a profound impact on numerous scientific and technological advancements. Here’s a glimpse into the enduring legacy of these mathematical giants:
Modern Applications of Mathematical Theories
The theories and concepts developed by these mathematicians have found practical applications in various fields. For instance, Newton’s laws of motion and gravitation are fundamental to our understanding of celestial mechanics and space exploration. Gauss’ least squares method is widely used in fields such as statistics, econometrics, and image processing.
Euler's work on graph theory has numerous applications in computer science, network analysis, and operations research. His work on number theory also has practical applications in cryptography, an essential component of secure digital communications.
Educational Influence
The teachings and methods of these mathematical masters continue to shape educational curricula worldwide. Newton’s calculus, Gauss’ contributions to statistics and number theory, and Euler’s work on geometry and trigonometry are all integral parts of modern mathematics education.
The principles and techniques developed by these mathematicians provide a solid foundation for students to build upon. Their work continues to inspire and challenge future generations of mathematicians and scientists, fostering a deeper understanding of the mathematical world.
Furthering Mathematical Research
The contributions of these mathematicians have opened new avenues of research and exploration in the field. Their work has provided a springboard for further mathematical inquiry, leading to the development of new theories and applications. The impact of their work continues to reverberate through the field of mathematics, driving innovation and progress.
Conclusion
The quest to identify the “best” mathematician is an intriguing exploration into the world of mathematical genius. Each of the mathematicians discussed here has made unparalleled contributions to the field, shaping the course of mathematics and influencing countless scientific advancements. Their work continues to inspire and guide mathematicians and scientists, driving the discipline forward.
From Newton's revolutionary calculus to Gauss' elegant proofs and Euler's profound formulas, the mathematical world is richer and more vibrant because of these luminaries. Their legacies endure, serving as a testament to the power of human intellect and the infinite possibilities within the realm of mathematics.
What is the fundamental theorem of algebra, and why is it significant?
+The fundamental theorem of algebra states that every non-constant single-variable polynomial with complex coefficients has at least one complex root. It is significant because it provides a fundamental understanding of the nature of polynomial equations and has implications for various areas of mathematics, including complex analysis and number theory.
How did Alan Turing’s work influence modern computing and artificial intelligence?
+Alan Turing’s work on the Turing machine, a theoretical device that can simulate the logic of any computer algorithm, laid the foundation for modern computing. His ideas and concepts influenced the development of computer hardware and software, and his research in cryptography and artificial intelligence continues to shape these fields today.
What is the significance of Euler’s formula, eiπ + 1 = 0, in mathematics?
+Euler’s formula, eiπ + 1 = 0, is considered one of the most beautiful and profound formulas in mathematics. It links five fundamental mathematical constants: e (the base of the natural logarithm), π (the ratio of a circle’s circumference to its diameter), i (the imaginary unit), 1, and 0. This formula encapsulates the harmony and interconnectedness of various mathematical concepts and has applications in complex analysis and physics.



