Coloring Graph
The act of coloring graphs is a fascinating and versatile technique in the realm of mathematics and computer science, offering a unique perspective on complex structures and their underlying patterns. Often overlooked as a mere visual aid, graph coloring holds a pivotal role in a multitude of applications, from optimizing resource allocation to analyzing social networks. As we delve deeper into the intricacies of this practice, we uncover a world where aesthetics and utility intertwine, revealing powerful insights and solutions.
Understanding Graph Coloring
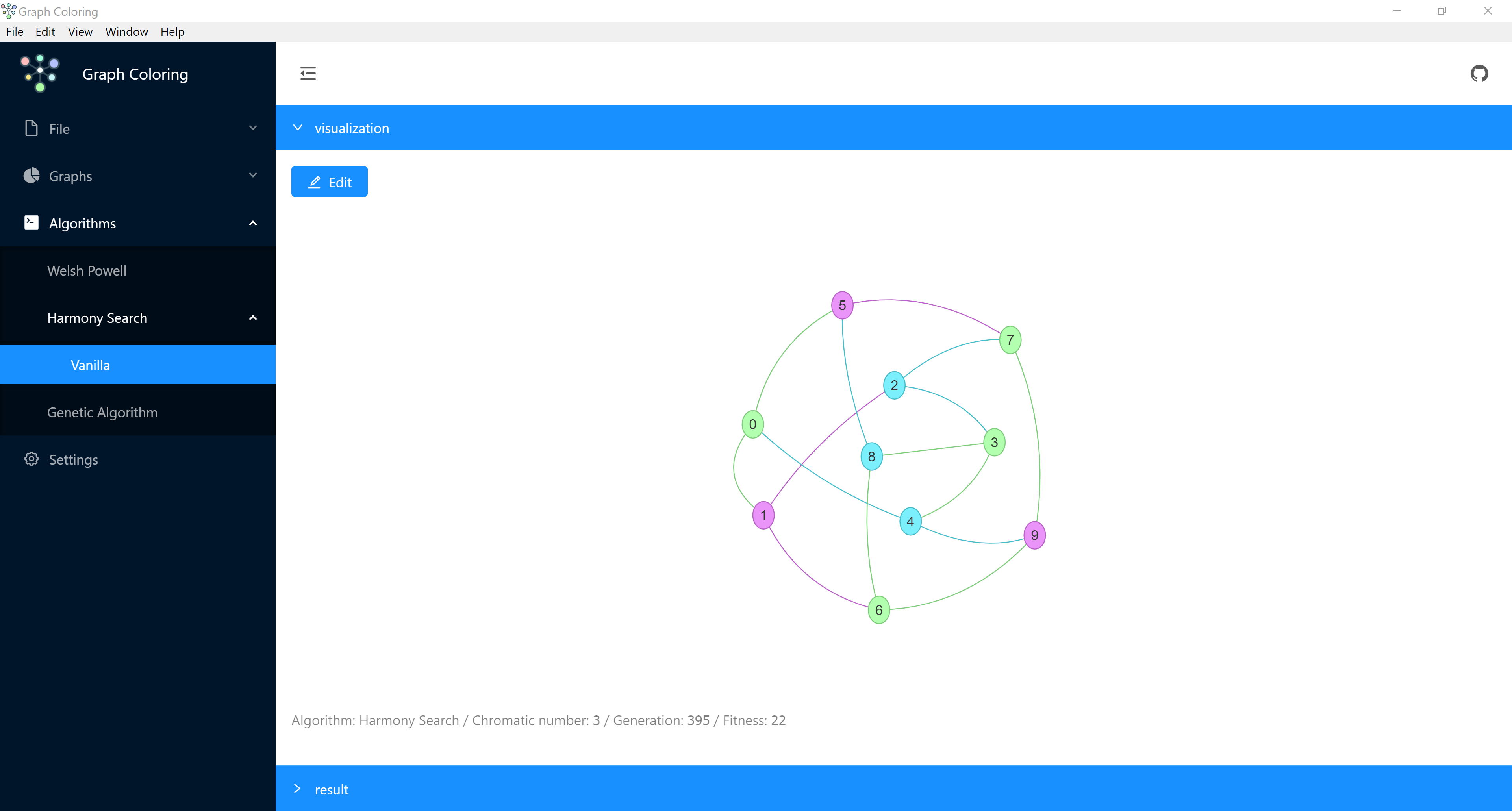
Graph coloring is an assignment of colors, or labels, to the vertices (or edges) of a graph such that no two adjacent vertices (or edges) have the same color. This seemingly simple concept has profound implications and applications in various fields. The primary objective is to use the minimum number of colors necessary to color a given graph, a problem known as the graph coloring problem.
Consider a social network where individuals are represented by vertices, and connections or friendships are denoted by edges. Graph coloring can help identify distinct groups or communities within this network by assigning unique colors to individuals who are not directly connected. This simple visualization aids in understanding the network's structure and dynamics, and it has profound implications for social network analysis.
Applications of Graph Coloring
The versatility of graph coloring extends far beyond social networks. In scheduling and timetabling, for instance, graph coloring is used to allocate resources and activities without conflicts. Consider a school’s timetable: graph coloring can ensure that no teacher is teaching multiple classes at the same time, and no student has overlapping classes. This application not only streamlines educational processes but also highlights the practical utility of graph coloring in everyday life.
In the realm of computer science, graph coloring is integral to the design and analysis of algorithms. It aids in optimizing search algorithms, designing efficient routing protocols, and even in the field of cybersecurity, where it can be used to identify potential vulnerabilities in complex networks.
| Field | Graph Coloring Application |
|---|---|
| Social Network Analysis | Identifying communities and patterns in social interactions |
| Scheduling and Timetabling | Optimizing resource allocation and activity planning |
| Computer Science Algorithms | Enhancing search algorithms, routing protocols, and cybersecurity |
Mathematical Foundation of Graph Coloring

At its core, graph coloring is a mathematical concept rooted in graph theory. A graph in this context is a collection of vertices (or nodes) and edges, where edges connect pairs of vertices. The challenge lies in assigning colors to these vertices (or edges) in a way that satisfies the coloring constraints.
The chromatic number of a graph is the minimum number of colors required to color it. Determining the chromatic number is a classic problem in graph theory, and its solution often involves sophisticated mathematical techniques. One such technique is the use of coloring algorithms, which provide efficient ways to assign colors to graphs, especially for large and complex networks.
Famous Graph Coloring Problems
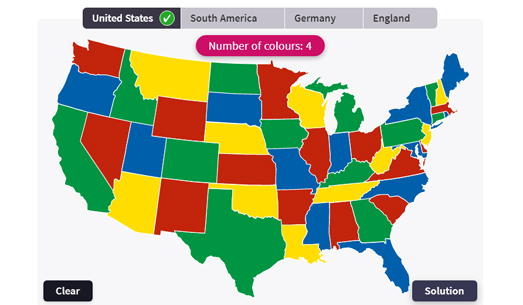
The history of graph coloring is dotted with famous problems that have challenged mathematicians for centuries. One such problem is the Four Color Theorem, which states that any map can be colored using only four colors such that adjacent regions have different colors. While this theorem was proven in the 1970s, it remains a cornerstone in the study of graph coloring.
Another notable problem is the Seven Color Theorem, which states that any planar graph (a graph that can be drawn in a plane without edge crossings) can be colored using at most seven colors. This theorem, though seemingly simple, has profound implications for the design and analysis of algorithms and has led to numerous advancements in the field.
| Theorem | Description |
|---|---|
| Four Color Theorem | Any map can be colored using four colors without adjacent regions having the same color. |
| Seven Color Theorem | Any planar graph can be colored using at most seven colors. |
Techniques and Algorithms
Efficient graph coloring is a delicate balance between mathematical theory and computational efficiency. Various techniques and algorithms have been developed to tackle this challenge, each with its strengths and limitations.
Greedy Coloring
One of the simplest and most intuitive algorithms is greedy coloring. This algorithm works by iteratively selecting the vertex with the fewest available colors and assigning it the lowest possible color. While this approach is straightforward, it may not always yield the optimal solution, especially for complex graphs.
Backtracking and Exact Algorithms
For more precise solutions, backtracking algorithms are employed. These algorithms explore all possible color combinations systematically, ensuring an optimal solution. However, their computational complexity can make them impractical for large graphs.
Heuristic and Metaheuristic Methods
In real-world applications, where computational efficiency is paramount, heuristic and metaheuristic methods are often preferred. These algorithms sacrifice some optimality for faster performance. Examples include genetic algorithms, simulated annealing, and tabu search, which mimic natural processes to find near-optimal solutions efficiently.
| Algorithm | Description |
|---|---|
| Greedy Coloring | Assigns colors iteratively based on the fewest available colors, a simple but not always optimal approach. |
| Backtracking | Explores all possible color combinations systematically, ensuring an optimal solution but with higher computational complexity. |
| Heuristic and Metaheuristic Methods | Provide efficient near-optimal solutions, often used in real-world applications where computational speed is crucial. |
Real-World Implications
The practical implications of graph coloring extend far beyond the realm of mathematics and computer science. In urban planning, for instance, graph coloring can help optimize land use by identifying areas with similar characteristics, aiding in efficient zoning and development planning.
In the field of logistics and transportation, graph coloring can be used to optimize routes and schedules, ensuring efficient delivery and reducing costs. It can also be applied to network design, helping to identify critical nodes and potential vulnerabilities in complex systems.
Future Prospects
As technology advances and data becomes more abundant, the potential for graph coloring to revolutionize various industries is immense. With the advent of big data and machine learning, graph coloring algorithms can be trained to recognize patterns and optimize solutions in real-time, opening up new avenues for efficiency and innovation.
Furthermore, the integration of graph coloring with other advanced mathematical techniques, such as network analysis and optimization, promises to deliver even more powerful tools for solving complex problems. The future of graph coloring is bright, with endless possibilities for application and innovation.
Conclusion

Graph coloring is a powerful tool with a broad range of applications, from understanding social networks to optimizing complex systems. Its ability to provide visual insights and optimize solutions makes it an indispensable technique in various fields. As we continue to explore and innovate, the potential for graph coloring to transform our understanding and management of complex systems is limitless.
What is the main purpose of graph coloring in mathematics and computer science?
+Graph coloring is primarily used to assign colors to the vertices (or edges) of a graph such that no two adjacent vertices (or edges) have the same color. This helps in understanding the structure of graphs and has various applications in optimization, scheduling, and network analysis.
How is graph coloring used in real-world applications?
+Graph coloring is applied in a wide range of fields, including social network analysis, urban planning, logistics, and transportation. It helps in optimizing resource allocation, identifying patterns and communities, and improving overall efficiency in complex systems.
What are some challenges associated with graph coloring algorithms?
+Graph coloring algorithms face challenges such as finding the optimal number of colors (chromatic number) and ensuring computational efficiency, especially for large and complex graphs. Trade-offs between optimality and speed are often made in real-world applications.



