5 Tips: Master the Midpoint Formula

In mathematics, the midpoint formula is a valuable tool that allows us to find the exact middle point between two distinct points on a line or in a coordinate system. This formula has wide-ranging applications, from simple geometry to complex engineering and scientific calculations. Mastering the midpoint formula is essential for anyone working with data, coordinates, or spatial relationships.
Today, we will delve into five expert tips to help you become proficient in using the midpoint formula. By understanding and applying these tips, you'll be able to solve problems efficiently and accurately, whether you're a student, researcher, or professional in fields like mathematics, physics, computer science, or engineering.
Understanding the Basics of the Midpoint Formula

The midpoint formula is a fundamental concept in mathematics, providing a straightforward method to calculate the midpoint of a line segment defined by two points. This formula is particularly useful when working with coordinates in a Cartesian plane, where we often need to determine the exact center point between two locations.
Mathematically, the midpoint formula is expressed as follows:
Midpoint(x, y) = ((x1 + x2) / 2, (y1 + y2) / 2)
Here, x1 and y1 represent the coordinates of the first point, while x2 and y2 are the coordinates of the second point. The formula essentially takes the average of the x and y coordinates to find the midpoint.
Let's look at a simple example. Suppose we have two points, (3, 4) and (7, 8). To find their midpoint, we apply the formula:
Midpoint = ((3 + 7) / 2, (4 + 8) / 2) = (5, 6)
So, the midpoint of these two points is (5, 6), which can be easily verified on a graph or coordinate plane.
Tip 1: Visualize the Problem
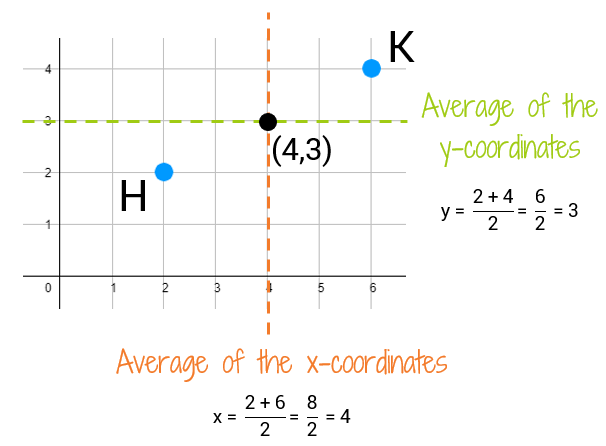
When working with the midpoint formula, it’s often helpful to visualize the problem. This means sketching the two points and the line segment that connects them on a coordinate plane. By doing so, you can gain a better understanding of the spatial relationship between the points and the resulting midpoint.
For instance, let's consider the points (-2, 3) and (4, -1). If we plot these points on a graph, we can see that they are quite far apart, both horizontally and vertically. Applying the midpoint formula, we get:
Midpoint = ((-2 + 4) / 2, (3 + (-1)) / 2) = (1, 1)
Indeed, the midpoint (1, 1) lies exactly in the middle of the line segment connecting the two original points. Visualizing the problem helps us confirm the accuracy of our calculations.
Tip 2: Understand the Formula’s Versatility
The midpoint formula is not limited to just two dimensions. It can be extended to higher dimensions, such as in three-dimensional space. In 3D, the formula becomes:
Midpoint(x, y, z) = ((x1 + x2) / 2, (y1 + y2) / 2, (z1 + z2) / 2)
Here, x1, y1, z1, and x2, y2, z2 represent the coordinates of the two points in 3D space. This extension of the formula allows us to find the midpoint between points in a three-dimensional coordinate system, which is particularly useful in fields like physics, engineering, and computer graphics.
For example, consider the points (1, 2, 3) and (5, 6, 7) in 3D space. Applying the 3D midpoint formula, we get:
Midpoint = ((1 + 5) / 2, (2 + 6) / 2, (3 + 7) / 2) = (3, 4, 5)
The midpoint (3, 4, 5) is located exactly in the middle of the line segment joining the two 3D points.
Tip 3: Practice with Different Scenarios
Mastering the midpoint formula requires practice. It’s beneficial to work through a variety of scenarios and problems to gain familiarity with the formula’s applications. Practice problems can range from simple two-dimensional coordinate calculations to more complex, real-world scenarios in three dimensions.
For instance, consider a real-world example in engineering. A bridge is being designed to connect two points, (100, 200) and (150, 300), on a river. The midpoint formula can be used to find the exact location of the center of the bridge, which is crucial for structural planning and construction.
Bridge Center = ((100 + 150) / 2, (200 + 300) / 2) = (125, 250)
By practicing with different scenarios, you'll not only improve your calculation skills but also enhance your understanding of how the midpoint formula is applied in various practical situations.
Tip 4: Explore Applications in Different Fields

The midpoint formula has a wide range of applications across various fields. Understanding these applications can provide additional context and motivation for learning and using the formula.
In physics, for example, the midpoint formula is used to calculate the center of mass of objects. In computer graphics, it helps determine the midpoint of a line segment in a 3D rendering engine. In data science, it can be used to find the average or mean value of two data points.
Consider the application in data science. Suppose we have two data points, 15 and 25, and we want to find their average. The midpoint formula can be adapted as follows:
Average = ((15 + 25) / 2) = 20
So, the average or mean of these two data points is 20. This simple application of the midpoint formula demonstrates its versatility and importance in data analysis and statistics.
Tip 5: Relate to Other Mathematical Concepts
The midpoint formula is closely related to other mathematical concepts, such as averages, means, and geometric properties. Understanding these connections can provide a deeper insight into the formula’s underlying principles and its role in mathematics.
For instance, the midpoint formula is directly related to the concept of the arithmetic mean. The arithmetic mean of two numbers is their sum divided by 2, which is precisely what the midpoint formula calculates for the coordinates of two points.
Additionally, in geometry, the midpoint of a line segment is equidistant from the two endpoints, which aligns with the concept of symmetry and balance in mathematical shapes and structures.
Conclusion
Mastering the midpoint formula is an essential skill for anyone working with data, coordinates, or spatial relationships. By understanding the basics, visualizing problems, exploring the formula’s versatility, practicing with diverse scenarios, and relating it to other mathematical concepts, you’ll become proficient in applying the midpoint formula in various contexts.
Whether you're a student, researcher, or professional, the midpoint formula is a powerful tool that will enhance your problem-solving abilities and contribute to your success in mathematics and its practical applications.
How is the midpoint formula used in real-world applications?
+The midpoint formula finds practical use in various fields. For instance, in engineering, it’s applied to determine the center of structures like bridges or buildings. In physics, it helps calculate the center of mass of objects. In computer graphics, it’s used to find the midpoint of line segments for rendering purposes. In data science and statistics, it’s employed to calculate the average or mean of data points.
Can the midpoint formula be extended to higher dimensions beyond 3D?
+Yes, the midpoint formula can be extended to higher dimensions. In n-dimensional space, the formula becomes: Midpoint(x1, x2, …, xn) = ((x1 + x2 + … + xn) / n). Here, x1, x2, …, xn represent the coordinates in the n-dimensional space. This extension allows for the calculation of midpoints in any number of dimensions.
What are some common mistakes to avoid when using the midpoint formula?
+Some common mistakes to avoid include mixing up the coordinates of the two points, not properly dividing by the number of points (2 in the case of the midpoint formula), and forgetting to account for negative numbers or large magnitudes when calculating averages or midpoints.



